Personal knowledge: it outweighs received knowledge

Our textbooks follow a conception different from those in standard textbooks. They are written with the belief that knowledge gained through personal reasoning has a higher quality than received knowledge. In our textbooks pupils discover mathematics themselves. The pathway of discovery takes the pupil from a personal experience to a concept. The pupil collects a range of experiences, which they talk about. He or she discusses the experiences with a classmate. They each explain their own theories, and subsequently test them on further problems. Throughout the process, they understand what they are doing.  

Big and small “Pythagorases“

Fine, you might think, the discovery path is obvious in this case, but what about “higher” mathematics?

By the age of 10, pupils have cut pizza into slices, they have cut paper, and fit various pieces into a pie, a circle, or a chocolate bar, and have solved a variety of problems involving similar topics.  They have never been told how to calculate part of a whole. Still, they know for certain how many minutes there are in a quarter, a third, a fifth, and two fifths of an hour. They know how to calculate both part of a whole and a whole from parts, in a range of situations.

A pupil is presented with a problem to find out how much 1/2 + 2/5 is. They may use, for example, a clock-face as an aid. They know that half an hour is 30 minutes. They know how to calculate that one fifth of an hour is 12 minutes, and so two fifths of an hour is 24 minutes. 24 minutes + 30 minutes is 54 minutes. They write 1/2 + 2/5 = 54/60. The numbers in this solution seem a bit high, so they reduce them, for instance by halving them. Now they have 27/30. The numbers can be further reduced to 9/10.

The pupil solves further problems in a similar fashion, records the solutions and discovers a trick. By creating a general mathematical pattern they discover “Pythagoras’ theorem” on their own. One pupil will find their “theorem” when they are ten, one between the ages of 11 to 14 in the fifth grade, another throughout grades six to nine; yet another pupil will not discover it at all: he or she will let a classmate explain it to them. They will think about it and accept it as their own. All three pupils, though, will discover the path not only to adding and reducing fractions, but also to mathematical patterns.  Most importantly, they see their activity as meaningful. These pupils, too, will eventually convert the given fraction to ones with a common denominator. At the same time, they understand why they do so and why it works as it does.  Their knowledge is permanent.

You can discover integrals

So how, you may ask, will high-school students discover integrals? People who ask this usually have the integrals they themselves learned in school in mind. These commonly correspond with the Weierstrass approach to integral calculus. That particular theory is built on rigorous logical principles, using so-called “epsilon delta” definitions.   

Our intention is to make use of more illustrative and more intuitive approaches, such as the Cavalieri principle. This principle is first discovered when calculating the area of triangles and the volume of solids. Later it can be used to experiment with areas of curvilinear objects defined by a parabola, a horizontal line and a vertical line (to be exact, lines that are parallel with the axes in the coordinate system), i.e. of certain “triangles with one bent side”. Students find out, for instance, how many times larger the blue object is than the red one. Next, they find out how many times larger the green object is than the blue one. By doing these calculations they discover the ratio for the areas of the red and green objects.  

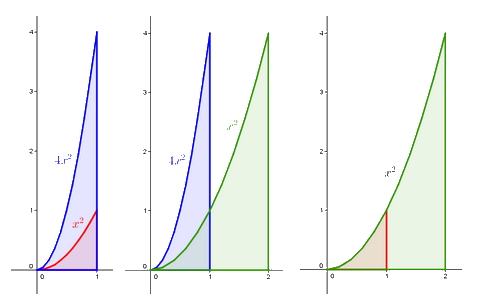
With the aid of further suitably chosen experiments, the students discover the trick for calculating the areas. Using the same trick, it is possible to find a method for calculating the area under many other curves and, finally, under any polynomial curve. In essence, this is what Cavalieri did two centuries before Weierstrass. By discovering these methods, students gain an understanding of the ideas underlying integral calculus.

From individual reasoning to accepting convention

Thanks to personal experience and logical reasoning, children are also ready and able to accept the conventional language of mathematics.  “Ah!,“ declares a 7 year old after discussing a series of experiences multiplying small numbers, “if I want to find out how many wheels there are on four tricycles, I don’t have to write 3 + 3 + 3 + 3. I can just use the times sign!” This pupil understands the multiplication operation and accepts its mathematical language. They are proud of themselves, and they look forward to new problems. The linguistic path to mathematical discovery can be summarized as:

EXPERIENCE ⇒ MOTHER TONGUE  ⇒ MATHEMATICAL LANGUAGE.